2024.05.11 2024.10.27

機械図面:幾何公差の疑問(幾何公差・普通幾何公差)

suu

技術ブロガーのスーです

本記事では、機械図面における幾何公差について解説していきます

「そもそも幾何公差って何？」

「幾何公差はなぜ必要なの？」

「幾何公差の種類は？」

「普通幾何公差って何？」

などの疑問にお答えします！

本記事を書くにあたって参考にした書籍

リンク

Contents

幾何公差とは？なぜ幾何公差が必要？
幾何公差の種類
普通幾何公差って何？
まとめ

幾何公差とは？なぜ幾何公差が必要？

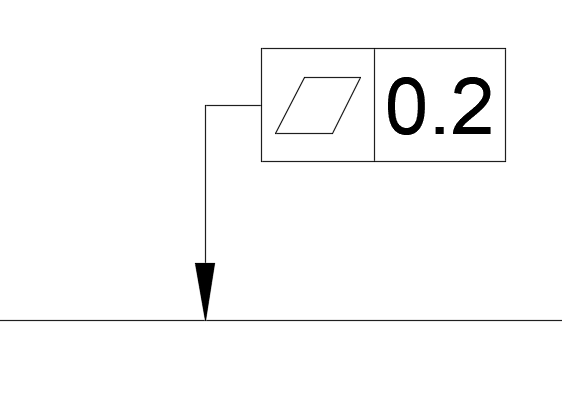
“幾何公差”とは、漢字の通り、幾何学的つまり形状に対して公差を設定します

例えば、できるだけ真円に加工したい部品に対して”真円度”という幾何公差を記入することで真円度合いを担保することが可能となります

しかし、幾何公差は寸法公差・はめあい公差よりも理解が難しく、記入方法や使用方法が難しいのが現実です

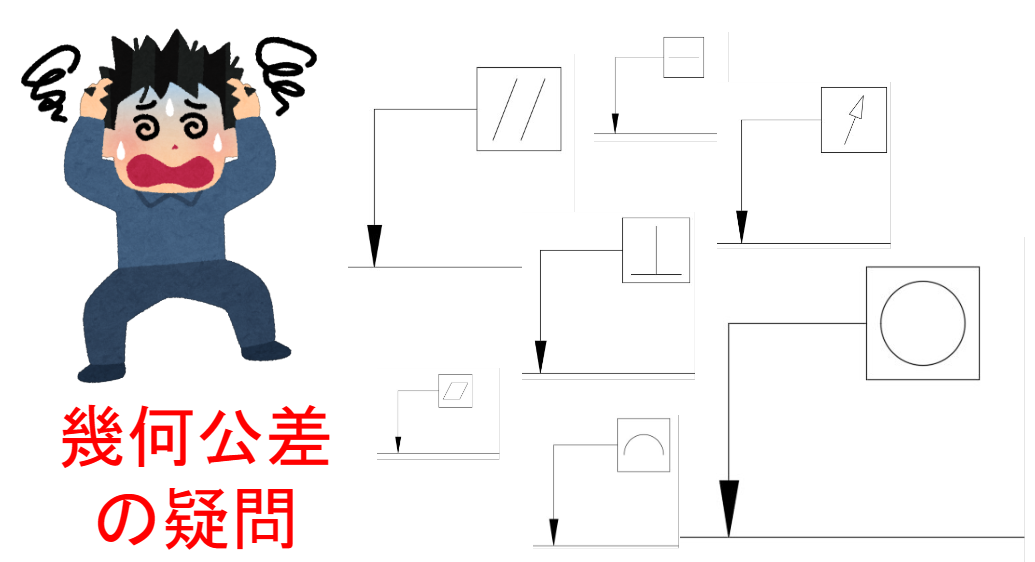
幾何公差の種類

幾何公差を理解するのが難しい理由の一つに、その種類の多さがあります

難しいうえに種類が多いので、私は今まで幾何公差を勉強することから避けていました…

各幾何公差についての詳しい説明は別にして、まずは幾何公差をざっと並べてみます

各幾何公差について一つ一つ解説するととんでもなく長い記事になってしまうので、本記事では割愛します

本記事を書くにあたって参考にした書籍

Amazon.co.jp: 図面の描き方がやさしくわかる本 : 西村仁: 本

本記事を書くにあたって参考にした本です

図面に関することがめちゃくちゃわかりやすくまとめてあるのでおすすめです

各幾何公差についても模式図を用いてわかりやすく解説してあるので参考にしてみて下さい！

形状公差(単独で指示)

真直度

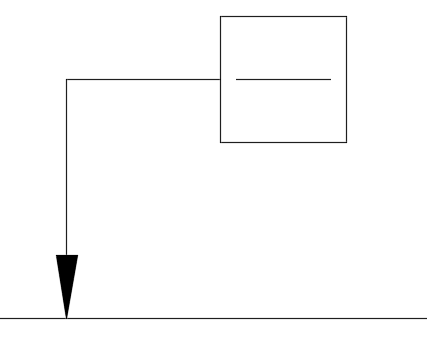
どれだけまっすぐであるべきかを表す幾何公差

平面度

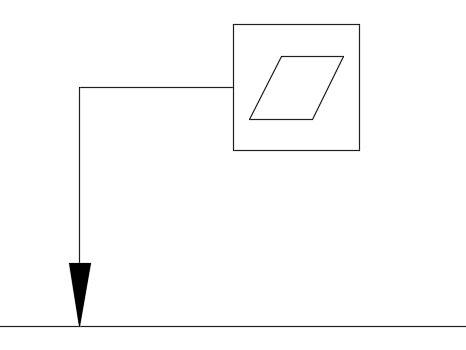
その面がどれだけ平らかどうかを表す幾何公差

真円度

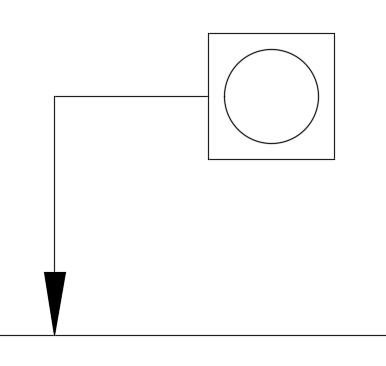
どれだけ真円であるべきかを表す幾何公差

円筒度

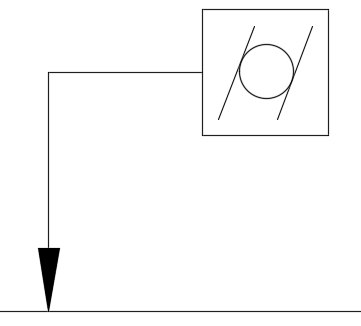
どれだけ円筒形状であるべきかを表す幾何公差

線の輪郭度

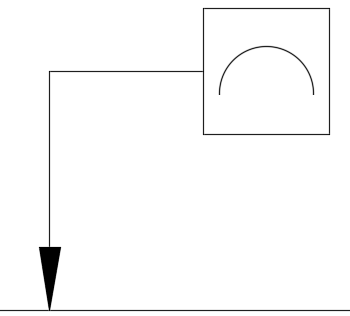
どれだけ指示した曲線に従うべきかを表す幾何公差

面の輪郭度

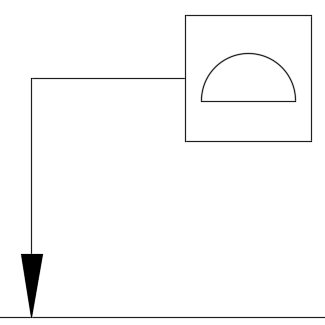
指示した面にどれだけ従うべきかを表した幾何公差

姿勢公差(ペアで指示)

平行度

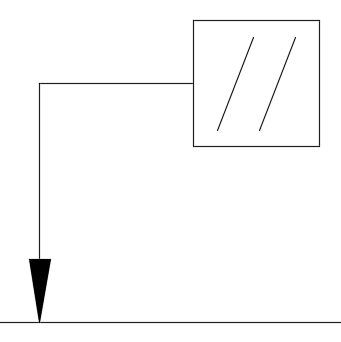
どれだけ平行であるべきかを表す幾何公差

直角度

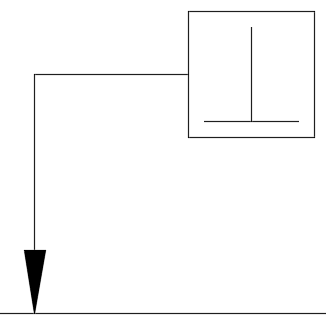
どれだけ直角であるべきかを表す幾何公差

傾斜度

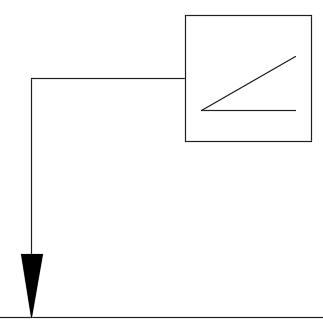
どれだけ指定した傾斜面であるべきかを表した幾何公差

位置公差(ペアで指示)

位置度

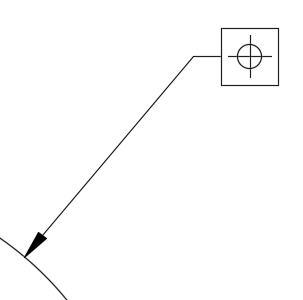
どれだけ指定した位置にあるべきかを表した幾何公差

同軸度

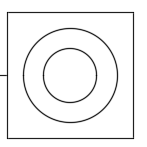
どれだけ同軸上にあるべきかを表した幾何公差

対称度

どれだけ中心面に対して対称であるべきかを表した幾何公差

振れ公差(ペアで指示)

円周振れ

1回転させたときの表面の一部がどれだけ振れないべきかを表した幾何公差

全振れ

1回転させたときの表面全体がどれだけ振れないべきかを表した幾何公差

普通幾何公差って何？

寸法公差にも普通公差がありこれは結構一般的で、少し機械設計に携わったことがあれば皆知っていると思います

幾何公差にも普通公差があることをご存じだったでしょうか？

私は恥ずかしながら、簡単な部品設計したことがなかったので最初は普通幾何公差の存在を知りませんでした(会社のフォーマットで知らず知らずのうちに表記していた)

普通幾何公差では何を指示しているのか？図面への表記方法などを解説していきます

まずは、JIS B 0419に示される普通幾何公差をざっと並べてみます

(JIS 0419 B : 1991 より抜粋)

真直度・平面度の普通公差

真直度・平面度の普通公差を上に示します

表内の数値の単位は寸法公差と同様mmです

また、表の最左列の公差等級に示される通り幾何公差の公差等級は、HKLで表されます

直角度の普通公差

上の表は直角度の普通公差を表します

直角度は面や辺がペアで必要となってくるため、どちらを呼び長さにするかという問題があります

JISでは短い方の辺を呼び長さとしています

従って、長い方の辺はデータムとなります

つまり、長い方の辺に対して短い方の辺がどれほど直角であるべきかの数値が上の表にまとめられています

対称度の普通公差

上の表は対称度の普通公差を表しています

直角度と同様長い方の辺がデータム、短い方の辺に対して普通公差の数値が決められています

円周振れの普通公差

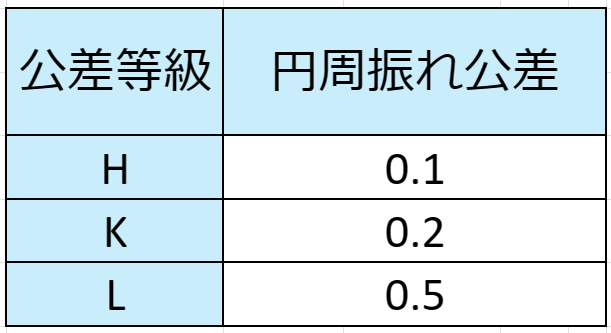
円周振れの普通公差を示します

円周振れに関しては、呼び長さによる区分がなく公差等級ごとに一律に決められます

真円度の普通公差

真円度の普通公差は直径の寸法公差の値と等しくとるが、半径方向の円周振れ普通公差の値を超えてはならない

円筒度の普通公差

円筒度の普通公差は、規定しない

平行度の普通公差

平行度の普通公差は、寸法公差と平面度公差・真直度公差とのいずれか大きいほうの値に等しくとる
二つの形体のうち長いほうをデータムとする。それらの形体が等しい呼び長さの場合には、いずれの形体をデータムとしてもよい

同軸度の普通公差

同軸度の普通公差は規定しない。

普通幾何公差の図面内への指示方法！

ここまで各幾何公差に対する普通公差についてJIS B 0419から抜粋してざっと並べてきました

では、具体的にどのような表記で図面内に指示すればよいのでしょうか？

図面内の注釈として、寸法公差の等級と共に指示します

(具体例) 普通幾何公差の図面内での指示方法

寸法の普通公差はmを指定したい場合
幾何公差の普通公差はKを指定したい場合

JIS 0419 B-mK

この表記を図面内に注釈として記載することで、この図面ではこの普通公差を適用してくださいというメッセージになります

まとめ

寸法公差やはめあい公差では指示しきれない部分を幾何公差で指示する！
幾何公差を使いこなすことで、より設計者の意図を伝えられる図面になる！
幾何公差は種類が豊富で、単独で指示する公差とペアで指示する公差がある！
寸法公差と同様に幾何公差にも普通幾何公差がある！
普通幾何公差の等級は寸法の普通公差の等級と一緒に指示する

ABOUT ME